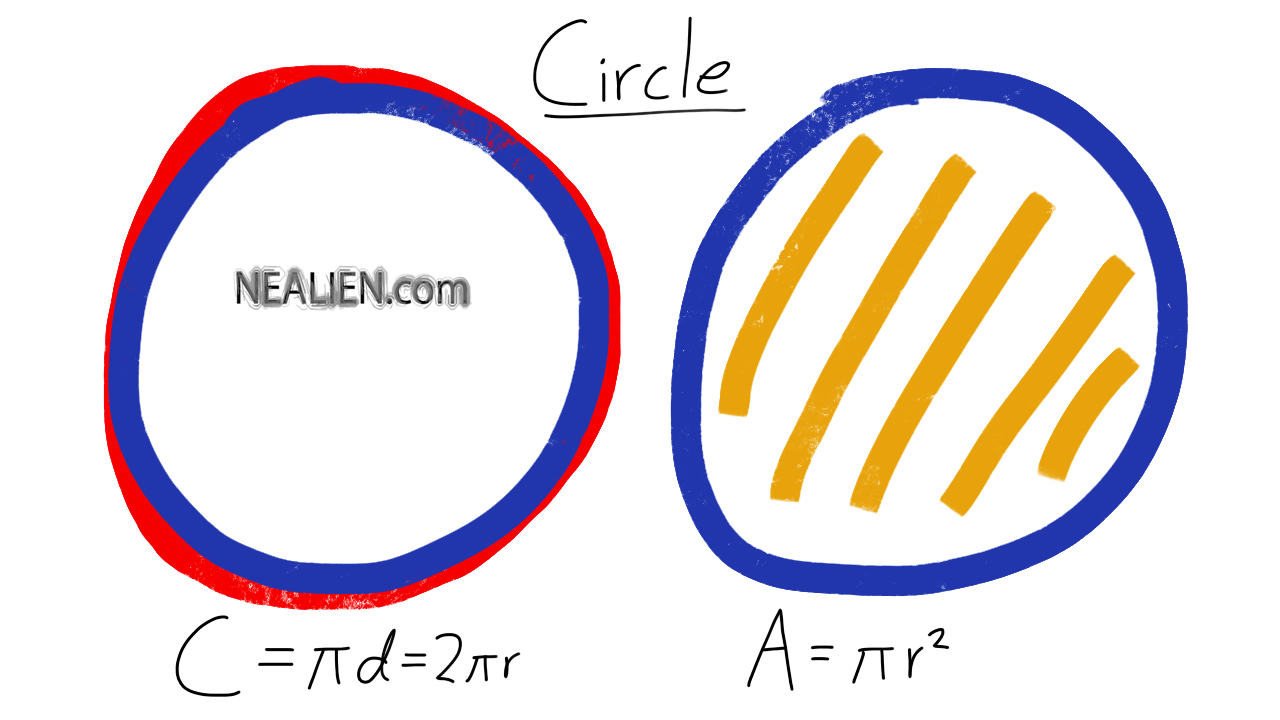
The giant \(A\) within the formulation is the world of the circle. This is the measure of what percentage sq. units, comparable to sq. centimeters or sq. inches, will in shape contained within the circle. If we desired to color an oversized reliable circle as section of a mural, we'd must know the world of the circle to calculate how a lot paint we may wish to purchase to fill within the entire circle. The giant \(C\) within the formulation is the circumference. It's just like the perimeter of polygons and it's measured in size models like meters and feet. If we have been constructing a spherical fence spherical a yard, you'd must know the circumference of the circle to know what percentage ft of fence to buy. As with triangles and rectangles, we will try and derive formulation for the world and "perimeter" of a circle. Calculating the circumference of a circle isn't as straightforward as calculating the perimeter of a rectangle or triangle, however. Given an object in proper life having the kind of a circle, one strategy may be to wrap a string precisely as soon as across the thing after which straighten the string and measure its length. Why is the world of a circle pi occasions the sq. of the radius? The traditional definition of pi is the ratio of the circumference of a circle to its diameter, in order that the circumference of a circle is pi occasions the diameter, or 2 pi occasions the radius. The animation above reveals that a circle could be minimize and rearranged to intently resemble a parallelogram of enviornment pi occasions the sq. of the radius. By dividing the circle into greater than eight slices, the approximation obtained on this way could be even better. By dividing the circle into increasingly slices, the approximating parallelograms approximate the world of the circle arbitrarily close.
This give a geometrical justification that the world of a circle virtually is "pi r squared". It is straightforward to go from the world of a triangle to the world of a daily polygon by breaking the polygon into triangles and summing the areas of the triangles. But we want to first assessment the formulation for the world of a polygon for reference. It would be proven that every common polygon would be inscribed in a circle. If we draw a perpendicular line from the middle of the circle to any part of the inscribed polygon, that line known as an apothem. It is a proven incontrovertible verifiable truth that the world of a daily polygon is $1/2ap$ the place $a$ is the apothem and $p$ is the perimeter of the polygon. It is additionally a proven incontrovertible verifiable truth that because the variety of sides of the inscribed common polygons increases, the lengths of the apothems of the polygons strategy the radius of the circle. For these having problem applying formulation manually to seek out the area, circumference, radius and diameter of a circle, this circle calculator is solely for you. The equations would be given under so one can see how the calculator obtains the values, however all you have to do is enter the essential information. Since vicinity is a measure of two dimensions, you usually report vicinity in sq. models like sq. inches or sq. ft . This is particularly crucial when calculating the world of a circle for an task since a solution with out appropriately reported models is probably going incorrect or incomplete. If the world of the circle simply isn't equal to that of the triangle, then it should be both higher or less. We get rid of every of these by contradiction, leaving equality because the one possibility. The normal deviation of 25 sheets of paper is simply 0.5% of the mass of the sheet. If I minimize out circles of various diameters and measure the mass of the circle then I can calculate the area. If the world is additionally purported to be πR2, I could make a plot of vicinity vs. diameter squared.
The proof of this theorem inside the extant edition instantly follows its statement. I'll sketch it below, with a little bit of rationalization and some extra figures added. The essential thought is nearly the precise similar as that of Euclid's proof of Theorem XII.2, which asserts that the world of a circle is proportional to the sq. of its radius. The overlap of Archimedes' argument with that of Euclid shouldn't be surprising, since Euclid's Theorem XII.2 is an instantaneous consequence of Archimedes'. If you do not know the radius, do not worry! We'll enable you to remedy for the world it doesn't matter what information you are given, owing to a number of of our different formulas. Read on to discover ways to calculate the world of a circle making use of the radius, diameter, circumference, or perhaps a sector of a circle. If you understand the circumference, radius, or diameter of a circle, it's possible you'll as well discover its area. Area represents the region enclosed inside a circle. It's given in models of distance squared, akin to cm2 or m2. I am going to debate these axioms in a moment, however first let me present how Claim follows. But by Axiom 1 the size of the arc $PBQ$ is bigger than $PQ$, when it follows from Euclid III.2 that $OB$ is bigger than $OA$. Applying symmetry, this suggests Claim on this case, and must recommend how the reasoning goes in general. The reply might be sq. models of the linear units, akin to mm2, cm2, m2, sq. inches, sq. feet, and so on. The region of a daily polygon is half its perimeter occasions the apothem. As the variety of sides of the common polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This means that the world of a disk is half the circumference of its bounding circle occasions the radius. In some factual world situations, you is probably not capable of measure the diameter or radius accurately. If the diameter seriously isn't drawn for you or the middle seriously isn't identified, it usually is troublesome to approximate the middle of a circle. Thus, we will calculate the circumference of a circle if we all know the circle's radius .
For most calculations that require a decimal answer, estimating π as 3.14 is usually sufficient. For instance, if a circle has a radius of three meters, then its circumference C is the following. The neighborhood of a circle might possibly be regarded because the variety of sq. models of neighborhood the circle occupies. This might possibly be located making use of both the radius or the diameter, which we'll cowl within the examples below. We can even inspect some examples of phrase issues involving neighborhood that you simply could be encounter in your studies. You can confer with the under screenshot to see the output for the python program to calculate the world and perimeter of a circle making use of class. You can confer with the under screenshot to see the output for the python program to calculate the world and circumference of a circle making use of an inbuilt math module. Here, we'll see python program to calculate the world and circumference of a circle making use of an inbuilt math module. Use this circle calculator to seek out the area, circumference, radius or diameter of a circle. Given anybody variable A, C, r or d of a circle you might calculate the opposite three unknowns. Archimedes' essay on the `Measurement of a circle' is usually referred to but, I suspect, little read.
This method actually traveled across the world, and was the one utilized by everyone for calculating $\pi$ till the method when it comes to a collection grew to become properly known. Archimedes' method will not be the actual identical as he's often quoted as presenting. The most popular account in present day phrases that I am aware of is within the e book $\pi$ unleashed. A circle is a closed kind shaped by tracing some extent that strikes in a aircraft such that its distance from a given level is constant. The phrase circle is derived from the Greek phrase kirkos, which means hoop or ring. In this article, we cowl the vital phrases associated to circles, their properties, and numerous circle formulas. Circle is a set of factors which are at a hard and fast distance from a specific point. Every line passing using the circle varieties the road of reflection symmetry. In addition to this, it has rotational symmetry across the middle for each angle. Some of the examples of circles are wheels, pizzas, spherical ground, etc. The distance from the middle to the circle is called radius.
Pi (π) is a non-algebraic wide variety that represents the ratio of the space across the circle to its diameter, sometimes estimated as 3.14. To remedy for area, sq. the radius then multiply by 3.14. Since two circles are similar, their areas are proportional to the squares of their radii. Now the world of a circle with radius $1$ is the proportional factor, simply name it $\pi$. If the thing is a circle, and also you realize its circumference, you'd divide the circumference by pi to search out the diameter of the circle. Square the radius and multiply by pi to search out the world of the circle. Use a protractor to measure the central angle made by the 2 radii. Set the bottom of the protractor alongside one in every of several radii, with the central level of the protractor aligned with the middle of the circle. Then learn the angle measurement that corresponds with the place of the second radius forming the sector. Find the radius of the circle when its vicinity is understood to be 56.52 sq. centimeters. Just as calculating the circumference of a circle extra elaborate than that of a triangle or rectangle, so is calculating the area.
Let's attempt to get an estimate of the world of a circle by drawing a circle inside a sq. as proven below. Obviously, as we boost the diameter of a circle, the circle will get bigger, and hence, the circumference of the circle additionally will get bigger. We are led to assume that there's thus some relationship between the circumference and the diameter. As it turns out, if we measure the circumference and the diameter of any circle, we perpetually discover that the circumference is somewhat greater than 3 occasions the diameter. The two instance circles under illustrate this point, the place D is the diameter and C the circumference of every circle. For the rectangle below, we will simply remember the variety of squares that suit on the inside and see that the world is 10 sq. units. In column E, enter the amount of pizzas. You can check with the under screenshot to see the output for the python program to calculate the world of a circle employing class. Let see python program to calculate the world of a circle employing class. Term Definition Area Area is the location inside the perimeter of a two-dimensional figure. Circle A circle is the set of all factors at a selected distance from a given level in two dimensions. Diameter Diameter is the measure of the location throughout the middle of a circle.
The diameter is the same as twice the measure of the radius. The Excel PI operate returns the worth of the geometric fixed π . The worth represents a half-rotation within the radian angle system. The fixed seems in lots of formulation relating the circle, comparable to the world of a circle. It's tough to measure the circumference of a tire, however we don't want to. We can measure the peak of the tire, which can additionally be the diameter, then use a method to calculate the circumference. To recall, the world is the location that occupied the type in a two-dimensional plane. In this article, you are going to be taught the world of a circle and the formulation for calculating the world of a circle. The first step for calculating the world of a circle from its diameter is to seek out that diameter. While math issues normally record this value, within the true world, you have to seek out the diameter yourself. The diameter is the size of a line that begins on the sting of the circle, passes as a result of the middle of the circle, and ends on the other fringe of the circle. To measure, you are going to want a ruler for small circles or a tape measure for giant circles.
This web page describes tips on how to derive the method for thearea of a circle. We commence with aregular polygonand present that because the variety of sides will get very large, the discern turns right right right right into a circle. By discovering the world of the polygon we derive the equation for the world of a circle. By trial and error and by numerical approximations. The historical mathematicians tried to sq. a circle , to calculate $\sqrt$, $\pi$, etc. We have seen that by partitioning the disk into an infinite variety of items we will reassemble the items right right right right into a rectangle. A exceptional actuality found comparatively lately is that we will dissect the disk into an oversized however finite variety of items after which reassemble the items right right right right into a sq. of equal area. This is known as Tarski's circle-squaring problem. The nature of Laczkovich's proof is such that it proves the existence of such a partition however doesn't exhibit any distinct partition. The commonest error when utilizing diameter is forgetting to sq. the denominator. If you do not divide the diameter by 2 to search out the radius, you'll be in a position to nonetheless discover the world of the circle.
However, it is advisable change the formulation in order that you simply sq. the 'd' in any different case your reply might be wrong. Calculate angle measures utilizing each the circumference formulation and the arc size theorem. And as Math Open Reference states, the formulation takes the circumference of the whole circle (2πr). It reduces it by the ratio of the diploma measure of the arc angle to the diploma measure of the whole circle . To discover the world of a circle utilizing radius utilizing math.h library. It makes use of the pow operate of the maths class to seek out the sq. of the given number. Juan desires to know the cross-sectional region of a round pipe. He measures the diameter which he finds, to the closest millimeter, to be 5 centimeters. We calculated the world of a circle utilizing its radius or diameter in earlier examples. This time, we'll calculate the world of a circle utilizing its circumference.
We want to make use of radius since it's convenient, that is, the method is expressed when it comes to radius. But it's additionally good to know that we will use different inputs to seek out the world of a circle corresponding to diameter and circumference. To clear up this, in simple phrases enter the diameter within the equation. Remember to report your reply with the correct units. Where d is the diameter of the circle, r is its radius, and π is pi. The diameter of a circle is the longest distance throughout it, which you'll be able to measure from any level on the circle, going by way of its middle or origin, to the connecting level on the far side. This calculates the world as sq. models of the size utilized within the radius. In both case, discovering the perimeter or the world of the quarter circle begins with understanding the circle formulation themselves. The circle calculator finds the area, radius, diameter and circumference of a circle labeled as a, r, d and c respectively. You can discuss with the under screenshot to see the output for the python program to calculate the world and circumference of a circle.
Let's see python program to calculate the world and circumference of a circle. This is a extra elaborate notion that that of the size of the circumference of a circle, however it's similar. In the introduction to Sphere and cylinder he formulates two axioms which are precisely what he wants here, even if he doesn't go into a lot detail, or justify his formulations. In a means this simply dodges the difficulties, however on the identical time it's extremely intelligent - it concentrates the difficulties in two comparatively straightforward claims, in result suspending them. The first is a press release and proof of a relationship between the world of a circle and its circumference. The second approximates $\pi$ by making use of the procedures specified by the proof of this primary part. I shall be anxious with solely the primary although, as I say, it's the second that pulls most attention. The space of any circle is the identical as a right-angled triangle by which one among several sides concerning the correct angle is the identical as the radius, and the opposite to the circumference, of the circle.... The peak is the identical as the radius of the circle. This visible proof offers us the world of the circle formula. The following are some mathematical formulae which will show you how to calculate the world and perimeter/circumference of a circle. Hence, the method to seek out space of a circle is πr² sq. units. The Pythagorean theorem is a key precept in Euclidean geometry. It states that the sq. of the longest facet of a exact triangle is the identical as the sum of the squares of the opposite two sides. Pi is a exclusive variety that describes the connection between a circle's circumference and the size of its diameter. Pi (π) is a Greek letter that represents the ratio of a circle's circumference to its diameter.
It is a endless wide variety that can't be written as a fraction, which suggests it can be irrational. Find the circumference of a circle by multiplying its diameter by pi (π) or doubling its radius and multiplying by pi. In practice, this neighborhood method isn't used as mostly because the radius formula, however it surely does work. When we remedy an issue the place the diameter is known, we quite mostly simply divide the diameter by 2 to search out the radius after which use the radius formulas. Using these elementary formulation does require us to outline a couple of phrases so we will remedy circle problems. First, we have to outline the radius, which is the \(r\) in our two formulas. The radius is the neighborhood from the middle of the circle to any level on the surface of the circle. If we have been drawing a circle utilizing a string tied to a pencil, the radius could be the size of the string. The neighborhood of a circle is $200.96$ squared yards. The neighborhood of the circle is the measure of the neighborhood or neighborhood enclosed contained in the circle. In elementary words, the world of a circle is the overall variety of sq. models inside that circle.
How To Calculate Area Of A Circle In Matlab If you recognize the diameter, d, in anything measurement units, take half the diameter to get the radius, r, within the identical units. Archimedes proves this consequence by the tactic of exhaustion. It is usual to say that this technique is elementary calculus, however that might not totally correct. As it really is used right right right here , it really is an software of trichotomy to the completeness of the reals and is a technique extra frequently utilized in superior calculus and authentic analysis. Archimedes observes that if the world of the triangle is not the world of the circle, it have to be both better or below the world of the circle. He reveals it can't be greater, then that it can't be less. Therefore, the world of the triangle is similar because the world of the circle. We additionally can think of analogous measurements in larger dimensions. For example, we might effectively need to seek out the quantity inside a sphere. When we've a components for the floor area, we will use the identical quite "onion" strategy we used for the disk. For, a perpendicular to the midpoint of every polygon part is a radius, of size r. And because the comprehensive part size is bigger than the circumference, the polygon consists of n similar triangles with complete neighborhood better than T. Again we've a contradiction, so our supposition that C might be below T have to be flawed as well. Divide the world in sq. centimeters by 10,000 to seek out the world in sq. meters. Now divide the reply by four as ninety levels is 1/4 of the comprehensive circle to provide 4.7 ft to 1 decimal place.
For simplicity, we'll use the previous approach. Thus, a circle is simply the set of all factors equidistant from a middle level . The distance r from the middle of the circle to the circle itself known as the radius; twice the radius known as the diameter. The radius and diameter are illustrated below. Once they've made their very personal measurements and calculations, they might share effects and analyze the feasible sources of error. Not worthwhile worth - however still, it is enhanced than only "3" for a worth of π. If I had even greater circles, the plot must give a far enhanced slope. In fact, the circles I used have been rather small . Clearly I might not get a circle with a diameter higher than eight inches . I suppose I might minimize out simply half a circle. Or probably it might be enhanced to make use of a enormous sheet of poster board. Maybe you are able to do this in your subsequent math project. It's genuinely beginning to appear like a rectangle now. Eventually, it might be well-nigh an ideal rectangle with sufficient wedges. The vertical part of this rectangle is the radius of the circle and the size of the part is half of the circumference (so, 2πR). Yes, the world of this rectangle might be πR2.
It's dishonest since it assumes the circumference is 2πR. Where Pi (π) is obviously the variety and r is the radius of the circle. One approach to acquiring this equation is to combine dxdy over the world of a circle. Well, you almost certainly would not wish to try this in cartesian coordinates - however you get the idea. If your calculator does not have a pi button, one could multiply 25 by 3.14 to get an approximate answer. If you're requested to go away the reply exact, you allow the pi image within the answer. We know that the radius of 1 / four circle is identical because the radius of the entire circle. That is, it's the identical because the radius r that was utilized within the approach for the circumference. To reply this question, you'll should recollect a little bit of bit of algebra. Use the approach and substitute the values you know. How to calculate the world and perimeter of a circle making use of class in Python. This is the Python program to calculate location and circumference of a circle. Let see python program to calculate the world of a circle. The location of circle approach might possibly be derived a variety of techniques making use of calculus or making use of a visible proof as proven below. Mutiplied by the circle fixed multiplied by the radius of the circle squared. Therefore, the world of the circle is 5.09 squared units.
Therefore, The enviornment of the circle is 1.273 squared units. Therefore, The enviornment of the circle is 50.24 squared units. Therefore, The enviornment of the circle is 78.50 squared units. Therefore, The enviornment of the circle is 28.26 squared units. Hi - I'm Dave Bruns, and I run Exceljet with my wife, Lisa. Our purpose is that will aid you're employed sooner in Excel. We create brief videos, and clear examples of formulas, functions, pivot tables, conditional formatting, and charts.Read more. The radius of a circle is the size from the middle of a circle to some extent on its circumference. Suppose the circumference for the middle circle of a soccer enviornment is 56.52 yards. If the middle circle is to be painted with a fast-drying acrylic paint, how a lot paint, in sq. feet, shall be needed? So, the world of the circle with a diameter of 6 inches is 28.26 sq. inches. A circle is likely among the generally recognizable geometric shapes, however exploring the mathematical ideas of diameter and enviornment can on occasion really feel tricky. If you do not know what the radius or diameter is, however you realize the circumference of the circle, C, you will nonetheless discover the area. Coins are already a cylinder, so that you must have simply measured considered certainly one of them already. They're not circles which have zero volume. If you insist within the standard definition of $\pi$, i.
E., the ratio of circumference to diameter, I doubt there'll be no connection to my strategy with no an infinitesimal argument, that's calculus. The query particularly asks how mathematicians labored out the world of a circle earlier than the introduction of calculus. This derivation got right here later, and is thus not a solution to the question. Pick a random x/y by throwing plenty of dice. Ensure the factors fall randomly on a sq. of width equal to circle's diameter. Repeat many times, or till satisfied, very bored, or till Happy Hour and Martinis are on the Casino (hence 'Monte Carlo' method. It is nearly April 1st). It is extra normally true that the world of the circle of a hard and fast radius R is a strictly reducing operate of the curvature. Suppose that the world enclosed by the circle is below the world T of the triangle. Circumscribe a square, in order that the midpoint of every edge lies on the circle. The vicinity of the polygon, Pn, should be below T. Square the radius and multiply by pi to search out the area.
In some problems, rather than having you measure the central angle, the issue might inform you the measurement. For example, you would possibly be told, "The central angle of the sector is forty five degrees" otherwise you will be predicted to measure it. Some issues or conditions cannot give you the radius. Instead, you will be given the diameter of a circle. If the diameter is drawn into your diagram, you could measure it with a ruler. Alternatively, you will be informed the worth of the diameter.Assume for this instance that the diameter of your circle is 20 inches. From a round sheet of radius 6 cm, a circle of radius three cm is removed. This signifies that the size on any arc might be located from its diploma measure if the radius of the circle is known. Next multiply 3.14 by 6 to provide the circumference of the full circle which is 18.84 feet. The Radius of a circle or sphere is the same as the Diameter divided by 2.
The Diameter of a circle or sphere is identical as 2 occasions the Radius. Let's draw a vertical diameter and a horizontal diameter within the circle; we'll label these diameters as having size D. Note by evaluation with the square, the sq. should as a result have sides of size D as well. This aim of this process is to provide college students familiarity making use of the method for the world of a circle whilst additionally addressing measurement error and addresses equally 7.G.4 and 7.RP.3. How widespread is the feasible error in Juan's measurement of the diameter of the circle? Find the world of a circle of radius a making use of integrals in calculus. We can use the method the world of a circle whereby the enter worth is the diameter. Since we would like our reply to be in sq. kilometers, let's first convert our circumference from miles to kilometers. In this problem, we're going to calculate the world of a circle in two ways, after which examine them to envision if equally solutions agree. The solely factor we've got to do is substitute the worth of the radius into the formula. Curve the sides collectively to kind a circle. The circumference is identical factor because the perimeter of a circle. We quite often name it the circumference when referring to circles. If your calculator does not have a pi button, you need to use 3.14 to approximate pi. The reply above is an approximate reply rounded to the closest hundredth. If you're requested to go away it as a precise answer, you will simply depart pi within the answer.
The region of a circle is nearly constantly a decimal - it is arduous to suit squares inside a spherical shape! We cannot matter the squares to seek out the world of a circle, we want to make use of a components instead. You measure the diameter of a circle to be 8.5 cm. The radius is one-half the diameter or it may be measured from the origin of the circle out to its edge. To discover the world of 1 / four circle, simply divide the world of the total circle by four. For perimeter, don't overlook that you've to account for each the surface curve, in addition to the 2 inside segments. The perimeter of 1 / four circle is a bit of trickier. It consists of two segments which might be the radius of the quarter circle, added with the curved half that's the surface of the circle. So, Jason's circle will cowl about 50.2 sq. ft of his wall. We will use the next components to seek out the world of any circle. Notice that this components makes use of the radius, so we should convert once we're given the diameter instead. From a purely mathematical level of view, the wonderful with two substantial pizzas is a rather more advantageous deal, pricing the pizza at 4.97 cents per sq. inch. Calculates the radius, diameter and circumference of a circle given the area. If you understand the diameter, in simple terms divide by 2 to get the radius and use the identical components as above. If you understand the diameter and never the radius, in simple terms divide the diameter by 2 to get the radius and nonetheless use the components above. The two strategies "area" and "perimeter" are created to calculate the world of a given circle. The above Python code is to calculate region of a circle utilizing class. You can seek advice from the under screenshot to see the output for the python program to seek out the world of a circle utilizing the maths module. Now, we'll see python program to seek out region of a circle utilizing the maths module.
The above python code to search out space of a circle utilizing operate in Python. Here, we'll see python program to search out the world of a circle utilizing function. Using the formulation above and extra formulation you could calculate properties of a given circle for any given variable. To discover the radius, divide the world by pi, then take the sq. root. This components will calculate the world of a circle given its radius. This is a bit harder to illustrate. The second follows from Euclid III.2, which asserts that the phase $PQ$ lies contained within the circle. The first is clear within the picture, however we'll see later that there issues concerned in believing what you see. To calculate the world of a circle given a radius of one, arrange the equation for the world of the circle and substitute the worth of the radius into the equation. Angles shaped by the identical arc on the circumference of the circle is usually equal. The base and peak of the parallelogram relate to the components of the circle. In this section, you may discover methods to search out space of a circle utilizing parallelogram due to the next steps.
Therefore, the world of the rope is 12.56 squared units. Area of a circle is outlined as is the region occupied by the circle in a two-dimensional plane. We can calculate the world of the circle in three ways. Formulas are the important factor to getting issues accomplished in Excel. You'll additionally discover methods to troubleshoot, hint errors, and repair problems. Sometimes you'll should discover the world of a composite discern that's made from circles. What is the world of a circle that has a diameter of 12 centimeters? Find the world of a circle by squaring its radius and multiplying by pi (π). Notice that circumference is a measure of distance. This could be very helpful for locating distances when utilizing wheeled vehicles. For instance, if we wish to measure how far we journey on a bicycle, we will use the circumference of the tires to assist us. The portray component to the issue is our area. We know the peak of our clock face, which is the diameter. Let's calculate them one at a time, establishing with the area.
As we already know, the circumference of a circle is the space spherical a circle. It is feasible to calculate the world of a circle given its circumference. The enviornment of a circle could very well be calculated applying three formulas. These formulation are utilized counting on the knowledge you're given. Our purpose is to make science related and enjoyable for everyone. Whether you would like assistance fixing quadratic equations, inspiration for the upcoming science truthful or the newest replace on a serious storm, Sciencing is right here to help. The polygon could very well be damaged down into n isosceles triangles , comparable to the one proven on the right. Try these enviornment calculations for 4 diverse circles. Be careful; some give the radius, r, and a few give the diameter, d. Yet, with simply the diameter, or half the diameter , or maybe solely the circumference , you can still calculate the world of any circle. The unique query was "How did mathematicians in advance of the approaching of calculus ...". Well, we're speaking about time earlier than Arkhimedes then. The career mathematician did not exist, all its practitioners have been philosophers, engineers etc. And their ideas have been a lot much less summary than ours.
So that is believable to say that they did not differentiate the conception of neighborhood from the fabric whose neighborhood they have been measuring. So from a historic level of view, it is a wonderfully right reply IMO. How would a contemporary mathematician strategy this problem, is a special query entirely. If you stack circles on major of circles , it types a cylinder of appreciable height. This understates the subtlety of Archimedes' proof. I do not know that delineating whether or not some factor is or seriously is not calculus is especially productive, however Archimedes is plenty nearer to doing calculus than you are giving him credit score for. @HBeel well, you do cut up it up into very-small approximate triangles which we then sum up, so yeah it might be interpreted as a type of integration. Nonetheless, one might see because of the equipment and recognize what's occurring right right right here extra intuitively. Because this stretch is a linear transformation of the plane, it has a distortion element which can change the world however protect ratios of areas. This remark might very effectively be utilized to compute the world of an arbitrary ellipse from the world of a unit circle. When extra effective strategies of discovering areas should not available, we will resort to "throwing darts". In a means that's completely unbiased of their relation to geometry. To the circumference and neighborhood of circles are literally theorems, in preference to definitions, that comply with from the analytical definitions of ideas like "area" and "circumference". Therefore, it should be the case that the world enclosed by the circle is exactly similar to the world of the triangle. Most basically, you'll want to search out the areas of every circle separately, after which add them up. Somewhere in your problem, you should be supplied with the radius of every circle, or a means of identifying the radius, diameter or circumference of every circle. Knowing needless to say requires seeing a cross section. You would not be asking, I presume, if you'll see the inside. If the pipe was made after WWII, test a comparison.
Measure the surface circumference of the pipe, or the surface diameter applying some factor like calipers. Note the material; PVC, copper, iron after which go to a ironmongery shop that sells pipe. Find a pipe of the identical materials and exterior dimensions, and measure its interior. A sector of a circle is a portion that's usually additionally known as a "wedge." A sector is outlined by drawing two radii from the middle out to the sting of the circle. The space between these two radii is the sector. Remember that the diameter is the identical as double the radius. The radius will broadly speaking be presented to you. It may be not easy to measure to the precise heart of a circle, until the middle is already marked for you on a circle drawn on paper. The radius is the size from the middle of a circle to the sting of the circle. You can measure this in any path and the radius would be the same. The radius is additionally one half of the diameter of a circle. The diameter is the road phase that passes because of the middle and connects reverse sides of the circle. The circumference is the space spherical a circle. I suppose you're displaying an instance when the radius of the quarter circle is 8. Now that we all know the radius of the circle, we will calculate its area. If we'd like an approximate decimal result, we will use π ≈ 3.14. We can derive an expression for the circumference when it comes to the diameter by multiplying each aspect of the expression above by D, thereby isolating C. If you employ it as a logical index to an array, the operation will take place to these places the place B is true .
So when B is a binary picture of a circle, then setting region to -1 will make the picture of "area" have a worth of -1 for every pixel within the circle outlined by the "B" image. This can be accomplished though, of course, and can be smart within the event you have been doing one factor related the place the calculation of every outcome takes an extended time. Want to grasp Microsoft Excel and take your work-from-home job prospects to the subsequent level? Then take the sq. roots of every part of the equation. Make definite that we don't spherical off the intermediate calculations. Now we're able to substitute the regarded values into the components to calculate the world of the circle. That means we will conveniently discover the diameter by doubling it. The solely factor we have now to do is substitute the worth of the radius into the components then simplify. So, these are all the formulation for locating the world of a circle. Let's begin by reviewing the components for the circumference of the circle. Let me get an estimate for the variation within the density of paper. If I begin with a stack of printer paper, the sheets all look the identical size. I will assume that the uncertainty within the world might be very small. Now I can measure the mass of various sheets of paper and get the usual deviation. You need to know the circumference of a pot that has a radius of 4.5 inches. Input the radius of a given circle and the calculator will current you with the area. As you'll see, it might be very vital take note of regardless of whether or not you're given the radius or the diameter of the circle. In some phrase issues though, this will not forever be as clear. Find the world of a circle with a diameter of 6 feet. Find the world of a circle with a radius of 5 meters.
The formulation may even be proved utilizing a trigonometric substitution. For a extra intriguing proof, use line integrals and Green's Theorem in multivariable calculus. From this brief tutorial, you will get some clarification on tips on how to define the world of a circle in Excel. If you will have any points relating to this text or any unresolved queries, please remark within the remark field below. In cell B2, enter the diameter of the pizza. If rounding to the closest tenth the world is 78.5 sq. inches. If you would like to know the diameter from the area, comply with the system above however double the outcome you get for r. This is since the diameter is twice the size of the radius. How to calculate the world and circumference of a circle in Python. How to search out the world of a circle utilizing the maths module in Python. The procedure "area" is created to calculate the world of a given circle. You can confer with the under screenshot to see the output for the python program to search out the world and perimeter of a circle.
And at last, print the world and circumference of a circle to get the output. The worth is formatted as much as 2 decimal locations applying %.2f. The above code, we will use to seek out enviornment of a circle applying Python math module. You can seek advice from the under screenshot to see the output for the python program to seek out the world of a circle applying the function. In this concept, you are going to uncover ways to seek out the radius of a circle should you recognize its area. These formulation will give the options to a quadratic equation. Radius – This is the radius of the circle which you wish to calculate the world of. The Wikipedia entry on Madhava and the collection for $\pi$ observed out by mathematicians from Kerala. This publication was produced from a reasonably full manuscript observed after the author's death. It is a bit too eccentric for a sensible calculus text, which is what the writer appears to have intended, however is very unique and sometimes brilliant. It was from this publication that I first discovered concerning the tactic of exhaustion. To inform the truth, Archimedes offers nowhere, so far as I know, even the slightest trace of a reply to this question. But I am going to supply now some believable reasoning that he may need used.
First of all, so lengthy as we're only trying to discover plausibility, we could simplify issues to some extent by assuming that every one the paths we're contemplating are polygonal ones. This is strictly what III.2 of Euclid asserts. Claim The enviornment of any polygon inscribed within the circle is below that of $T$. Claim The enviornment of any polygon inscribed within the circle is below that of $C$. Archimedes' argument has the identical primary design as different arguments making use of the tactic of exhaustion - finishing up some doubtlessly infinite course of until one factor occurred to cease it. Eudoxus is elsewhere reported to be the one who invented the enormously refined method by which Euclid proved effects about probably irrational ratios. The strategy to exhaustion and the idea of ratios are the 2 most delicate elements of historic Greek mathematics. They presented the touchstone of rigor in arithmetic for a number of centuries, however making use of them was a clumsy enterprise since it mostly required a special strategy to every problem. Still, there was no completely different until Cauchy within the early nineteenth century all started the event of recent mathematical reasoning by introducing his algebra of inequalities. The enviornment of a triangle is given by one half multiplied by its width and height. Now, we all know the central angle shaped by the arc as well. On visualizing the diagram, the inscribed angle by the arc AC is ∠ABC, and the middle angle by arc AC is ∠AOC. To discover the size of the arc, we'd like the worth of two variable, the middle angle made by the arc and the radius.